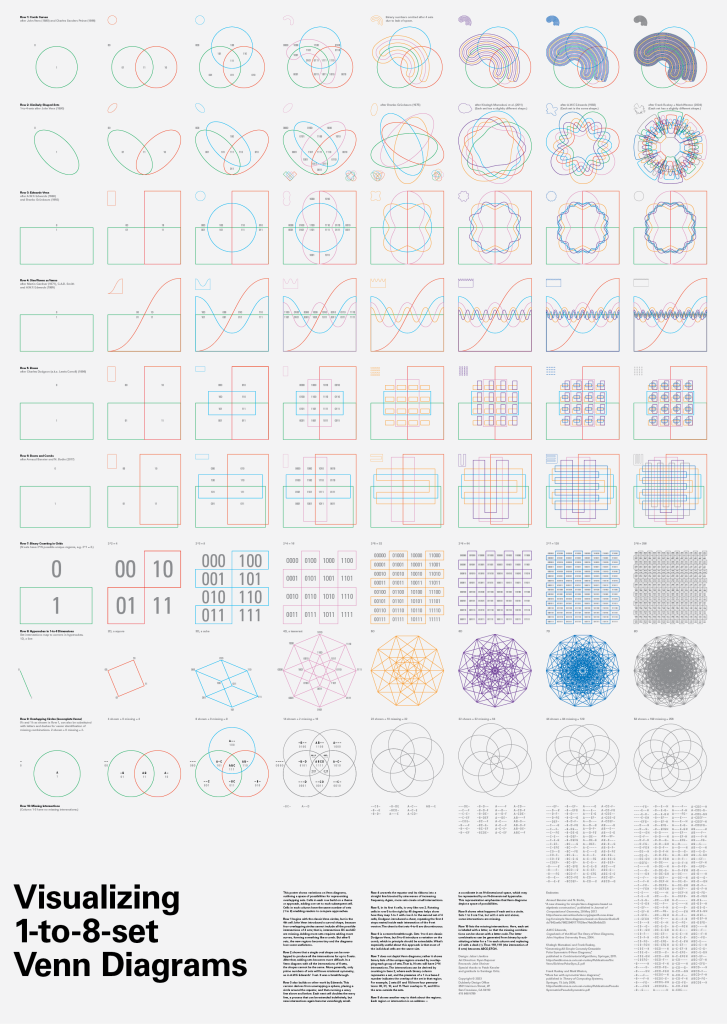
This poster shows variations on Venn diagrams, outlining a space of possibilities for representing overlapping sets. Cells in each row build on a theme or approach, adding one set to each subsequent cell. Cells in each column have the same number of sets (1 to 8) enabling readers to compare approaches.

Row 1 begins with the classic Venn circles, but in the 4th cell John Venn introduced a curved shape, because four overlapping circles cannot include all the possible intersections of 4 sets; that is, intersections BC and AD are missing. Adding more sets requires adding more curves, forming something like a comb. But after 5 sets, the new regions become tiny and the diagrams lose some usefulness.

Row 2 shows that a single oval shape can be overlapped to produce all the intersections for up to 5 sets. After that, adding sets becomes more difficult. In a Venn diagram with all the intersections of 6 sets, the shapes cannot be the same. More generally, only prime numbers of sets will have rotational symmetry, as in A.W.F. Edwards’ 7-set. It was a breakthrough.

Row 3 also builds on other work by Edwards.This version derives from unwrapping a sphere, placing a circle around the equator, and then running a wavy line above and below. Each next cell doubles the wavy line, a process that can be extended indefinitely, but new intersections again become vanishingly small.

Row 4 unravels the equator and its ribbons into a straight line bisected by sine waves of increasing frequency. Again, more sets create small intersections.

Row 5, in its first 4 cells, is very like row 2. Rotating cells in row 5 to the right by 45 degrees helps show how they map 1-to-1 with row 2. In the second set of 4 cells, Dodgson introduced a cheat, repeating the first 4 steps nested inside each intersection of the 4-set version.The cheat is that sets 4-to-8 are discontinuous.

Row 6 is a recent breakthrough. Sets 1-to-4 are classic Dodgson-Venn, but 5-to-8 introduce a variation on the comb, which in principle should be extendable. What’s especially useful about this approach is that most of the individual cells are the same size.

Row 7 does not depict Venn diagrams; rather it shows binary lists of the unique regions created by overlapping each group of sets. That is, N sets will have 2^N intersections. The intersections can be derived by counting in base 2, where each binary column represents a set, and the presence of a 1 in a base-2 number indicates the overlap of the set in that region. For example, 2 sets (01 and 10) have four permutations: 00, 01, 10, and 11. Their overlap is 11, and 00 is the area outside the sets.

Row 8 shows another way to think about the regions. Each region or intersection is an address — a coordinate in an N-dimensional space, which may be represented by an N-dimensional hypercube. This representation emphasizes that Venn diagrams depict a space of possibilities.

Row 9 shows what happens if each set is a circle. Sets 1 to 3 are fine, but with 4 sets and above, some intersections are missing.

Row 10 lists the missing intersections. Here, each set is labeled with a letter, so that the missing combinations can be shown with a letter code.The letter combinations can be generated from binary by substituting a letter for a 1 in each column and replacing a 0 with a dash (–). Thus 1111,1111 (the intersection of 8 sets) becomes ABCD,EFGH.

Download PDF

Endnotes

Arnaud Bannier and N. Bodin, “A new drawing for simple Venn diagrams based on algebraic construction,” published in Journal of Computational Geometry, 29 May 2017. https://www.semanticscholar.org/paper/A-new-drawing-for-simple-Venn-diagrams-based-on-Bannier-Bodin/8dc7542ae0c786229401777029ee74ab26e6dd23

A.W.F. Edwards, Cogwheels of the Mind: The Story of Venn Diagrams, John Hopkins University Press, 2004.

Khalegh Mamakani and Frank Ruskey, “Generating All Simple Convexly-Drawable Polar Symmetric 6-Venn Diagrams,” published in Combinatorial Algorithms, Springer, 2011. https://webhome.cs.uvic.ca/~ruskey/Publications/SixVenn/SixVennPolarSym_E.pdf

Frank Ruskey and Mark Weston, “More fun with symmetric Venn diagrams,” published in Theory of Computing Systems, Springer, 13 July 2005. https://webhome.cs.uvic.ca/~ruskey/Publications/Pseudo Symmetric/PseudoSymmetric.pdf