*Written for Interactions magazine by Hugh Dubberly, Usman Haque, and Paul Pangaro.*
When we discuss computer-human interaction and design for interaction, do we agree on the meaning of the term “interaction”? Has the subject been fully explored? Is the definition settled?
**A Design-Theory View**
Meredith Davis has argued that interaction is not the special province of computers alone. She points out that printed books invite interaction and that designers consider how readers will interact with books. She cites Massimo Vignelli’s work on the *National Audubon Society Field Guide to North American Birds* as an example of particularly thoughtful design for interaction [1].
Richard Buchanan shares Davis’s broad view of interaction. Buchanan contrasts earlier design frames (a focus on form and, more recently, a focus on meaning and context) with a relatively new design frame (a focus on interaction) [2]. Interaction is a way of framing the relationship between people and objects designed for them—and thus a way of framing the activity of design. All man-made objects offer the possibility for interaction, and all design activities can be viewed as design for interaction. The same is true not only of objects but also of spaces, messages, and systems. Interaction is a key aspect of function, and function is a key aspect of design.
Davis and Buchanan expand the way we look at design and suggest that artifact-human interaction be a criterion for evaluating the results of all design work. Their point of view raises the question:
Is interaction with a static object different from interaction with a dynamic system?
**An HCI View**
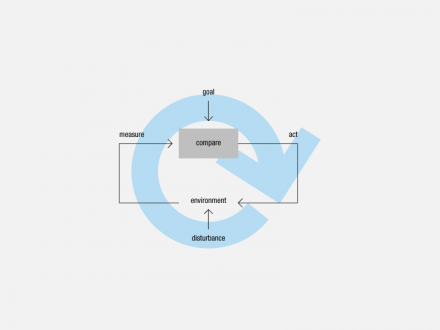
Canonical models of computer-human interaction are based on an archetypal structure—the feedback loop. Information flows from a system (perhaps a computer or a car) through a person and back through the system again. The person has a goal; she acts to achieve it in an environment (provides input to the system); she measures the effect of her action on the environment (interprets output from the system—feedback) and then compares result with goal. The comparison (yielding difference or congruence) directs her next action, beginning the cycle again. This is a simple self-correcting system—more technically, a first-order cybernetic system.
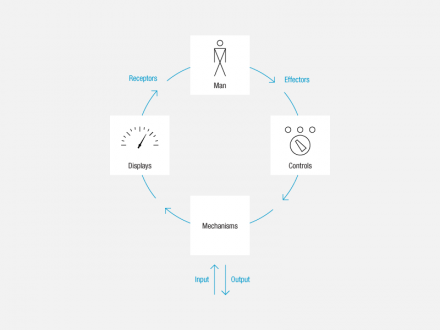
In 1964 the HfG Ulm published a model of interaction depicting an information loop running from system through human and back through the system [3].
Man-Machine System
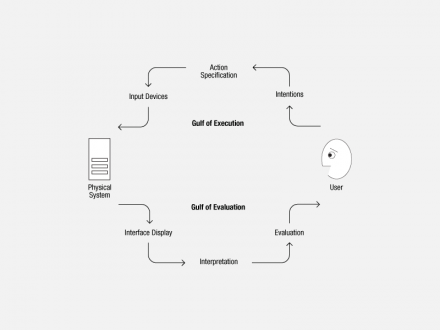
Gulf of Execution and Evaluation
Don Norman has proposed a “gulf model” of interaction. A “gulf of execution” and a “gulf of evaluation” separate a user and a physical system. The user turns intention to action via an input device connected to the physical system. The physical system presents signals, which the user interprets and evaluates—presumably in relation to intention [4].
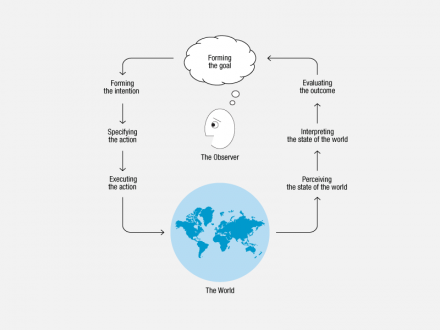
Norman has also proposed a “seven stages of action” model, a variation and elaboration on the gulf model [5]. Norman points out that “behavior can be bottom up, in which an event in the world triggers the cycle, or top-down, in which a thought establishes a goal and triggers the cycle. If you don’t say it, people tend to think all behavior starts with a goal. It doesn’t—it can be a response to the environment. (It is also recursive: goals and actions trigger subgoals and sub-actions) [6].”
Seven Stages of Action
Interaction
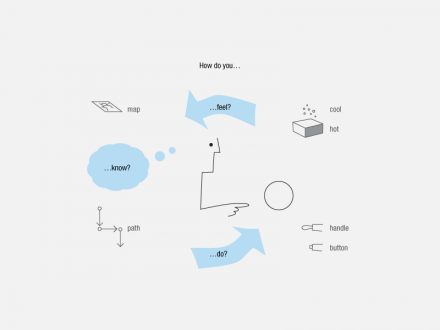
Like Norman’s models, Bill Verplank’s wonderful “How do you…feel-know-do?” model of interaction is also a classic feedback loop. Feeling and doing bridge the gap between user and system [7].
Representing interaction between a person and a dynamic system as a simple feedback loop is a good first approximation. It forefronts the role of information looping through both person and system [8]. Perhaps more important, it asks us to consider the user’s goal, placing the goal in the context of information theory—thus anchoring our intuition of the value of Alan Cooper’s persona-goal-scenario design method [9].
In the feedback-loop model of interaction, a person is closely coupled with a dynamic system. The nature of the system is unspecified. (The nature of the human is unspecified, too!) The feedback-loop model of interaction raises three questions: What is the nature of the dynamic system? What is the nature of the human? Do different types of dynamic systems enable different types of interaction?
**A Systems-Theory View**
The discussion that gave rise to this article began when Usman Haque observed that “designers often use the word ‘interactive’ to describe systems that simply react to input,” for example, describing a set of Web pages connected by hyperlinks as “interactive multimedia.” Haque argues that the process of clicking on a link to summon a new webpage is not “interaction”; it is “reaction.” The client-server system behind the link reacts automatically to input, just as a supermarket door opens automatically as you step on the mat in front of it.
Haque argued that “in ‘reaction’ the transfer function (which couples input to output) is fixed; in ‘interaction’ the transfer function is dynamic, i.e., in ‘interaction’ the precise way that ‘input affects output’ can itself change; moreover in some categories of ‘interaction’ that which is classed as ‘input’ or ‘output’ can also change, even for a continuous system [10].”
For example, James Watt’s fly-ball governor regulates the flow of steam to a piston turning a wheel. The wheel moves a pulley that drives the fly-ball governor. As the wheel turns faster, the governor uses a mechanical linkage to narrow the aperture of the steam-valve; with less steam the piston fills less quickly, turning the wheel less quickly. As the wheel slows, the governor expands the valve aperture, increasing steam and thus increasing the speed of the wheel. The piston provides input to the wheel, but the governor translates the output of the wheel into input for the piston. This is a self-regulating system, maintaining the speed of the wheel—a classic feedback loop.
Of course, the steam engine does not operate entirely on its own. It receives its “goal” from outside; a person sets the speed of the wheel by adjusting the length of the linkage connecting the fly-ball governor to the steam valve. In Haque’s terminology, the transfer function is changed.
Our model of the steam engine has the same underlying structure as the classic model of interaction described earlier! Both are closed information loops, self-regulating systems, first-order cybernetic systems. While the feedback loop is a useful first approximation of human computer interaction, its similarity to a steam engine may give us pause.
The computer-human interaction loop differs from the steam-engine-governor interaction loop in two major ways. First, the role of the person: The person is inside the computer-human interaction loop, while the person is outside the steam-engine-governor interaction loop. Second, the nature of the system: The computer is not characterized in our model of computer-human interaction. All we know is that the computer acts on input and provides output. But we have characterized the steam engine in some detail as a self-regulating system. Suppose we characterize the computer with the same level of detail as the steam engine? Suppose we also characterize the person?
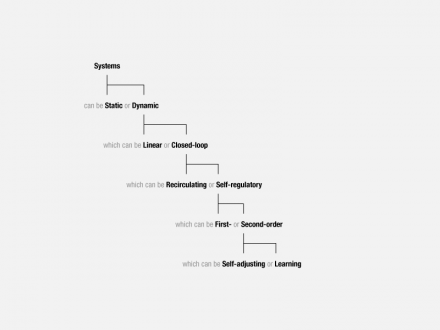
**Types of Systems**
So far, we have distinguished between static and dynamic systems—those that cannot act and thus have little or no meaningful effect on their environment (a chair, for example) and those that can and do act, thus changing their relationship
to the environment.
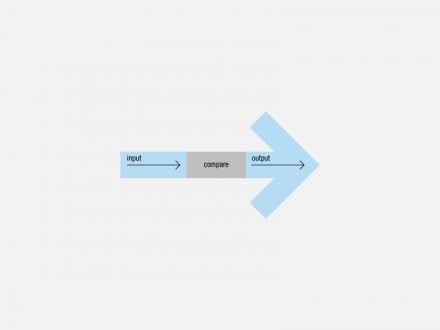
Within dynamic systems, we have distinguished between those that only react and those that interact—linear (open-loop) and closed-loop systems.
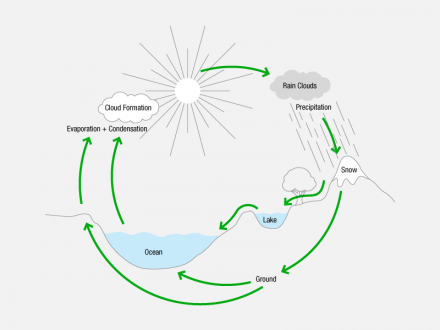
Some closed-loop systems have a novel property—they can be self-regulating. But not all closed-loop systems are self-regulating. The natural cycle of water is a loop. Rain falls from the atmosphere and is absorbed into the ground or runs into the sea. Water on the ground or in the sea evaporates into the atmosphere. But nowhere within the cycle is there a goal.
Types of Systems
A self-regulating system has a goal. The goal defines a relationship between the system and its environment, which the system seeks to attain and maintain. This relationship is what the system regulates, what it seeks to keep constant in the face of external forces. A simple self-regulating system (one with only a single loop) cannot adjust its own goal; its goal can be adjusted only by something outside the system. Such single-loop systems are called “first order.”
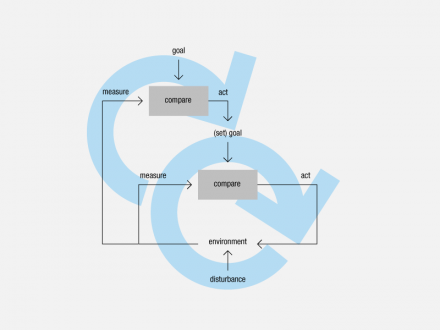
Learning systems nest a first self-regulating system inside a second self-regulating system. The second system measures the effect of the first system on the environment and adjusts the first system’s goal according to how well its own second-order goal is being met. The second system sets the goal of the first, based on external action. We may call this learning—modification of goals based on the effect of actions. Learning systems are also called second-order systems.
Some learning systems nest multiple self-regulating systems at the first level. In pursuing its own goal, the second-order system may choose which first-order systems to activate. As the second-order system pursues its goal and tests options, it learns how its actions affect the environment. “Learning” means knowing which first-order systems can counter which disturbances by remembering those that succeeded in the past.
Water Cycle
Linear system
Self-regulating system
Learning system
A second-order system may in turn be nested within another self-regulating system. This process may continue for additional levels. For convenience, the term “second-order system” sometimes refers to any higher-order system, regardless of the number of levels, because from the perspective of the higher system, the lower systems are treated as if they were simply first-order systems. However, Douglas Englebart and John Rheinfrank have suggested that learning, at least within organizations, may require three levels of feedback:
+ basic processes, which are regulated by first-order loops
+ processes for improving the regulation of basic processes
+ processes for identifying and sharing processes for improving the regulation of basic processes
Of course, division of dynamic systems into three types is arbitrary. We might make finer distinctions. Artist-researcher Douglas Edric Stanley has referred to a “moral compass” or scale for interactivity “Reactive > Automatic > Interactive > Instrument > Platform” [11].
Cornock and Edmonds have proposed five distinctions:
(a) Static system
(b) Dynamic-passive system
(c) Dynamic-interactive system
(d) Dynamic-interactive system (varying)
(e) Matrix [12]
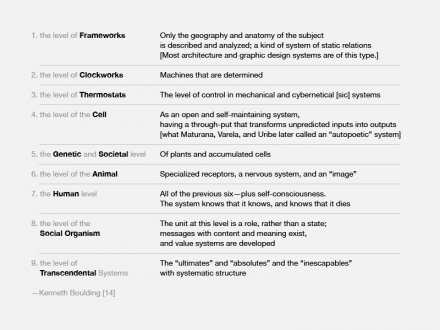
Kenneth Boulding distinguishes nine types of systems [13].
Levels of systems
System Combinations
————–
One way to characterize types of interactions is by looking at ways in which systems can be coupled together to interact. For example, we might characterize interaction between a person and a steam engine as a learning system coupled to a self-regulating system. How should we characterize computer-human interaction? A person is certainly a learning system, but what is a computer? Is it a simple linear process? A self-regulating system? Or could it perhaps also be a learning system?
Working out all the interactions implied by combining the many types of systems in Boulding’s model is beyond the scope of this paper. But we might work out the combinations afforded by a more modest list of dynamic systems: linear systems (0 order), self-regulating systems (first order), and learning systems (second order). They can be combined in six pairs: 0-0, 0-1, 0-2, 1-1, 1-2, 2-2.
**0-0 Reacting**
The output of one linear system provides input for another, e.g., a sensor signals a motor, which opens a supermarket door. Action causes reaction. The first system pushes the second. The second system has no choice in its response. In a sense, the two linear systems function as one.
This type of interaction is limited. We might call it pushing, poking, signaling, transferring, or reacting. Gordon Pask called this “it-referenced” interaction, because the controlling system treats the other like an “it”—the system receiving the poke cannot prevent the poke in the first place [15].
A special case of 0-0 has the output of the second (or third or more) systems fed back as input
to the first system. Such a loop might form a self-regulating system.
**0-1 Regulating**
The output of a linear system provides input for a self-regulating system. Input may be characterized as a disturbance, goal, or energy.
Input as “disturbance” is the main case. The linear system disturbs the relation the self-regulating system was set up to maintain with its environment. The self-regulating system acts to counter disturbances. In the case of the steam engine, a disturbance might be increased resistance to turning the wheel, as when a train goes up a hill.
Input as “goal” occurs less often. A linear system sets the goal of a self-regulating system. In this case, the linear system may be seen as part of the self-regulating system—a sort of dial. (Later we will discuss the system that turns the dial. See 1-2 below.)
Input as “energy” is another case, mentioned for completeness, though a different type than the previous two. A linear system fuels the processes at work in the self-regulating system; for example, electric current provides energy for a heater. Here, too, the linear system may be seen as part of the self-regulating system.
1-0 is the same as 0-1 or reduces to 0-0. Output from a self-regulating system may also be input to a linear system. If the output of the linear system is not sensed by the self-regulating system, then 1-0 is no different from 0-0. If the output of the simple process is measured by the self-regulating system, then the linear system maybe seen as part of the self-regulating system.
**0-2 Learning**
The output of a linear system provides input for a learning system. If the learning system also supplies input to the linear system, closing the loop, then the learning system may gauge the effect of its actions and “learn.”
On the other hand, if the loop is not closed, that is, if the learning system receives input from the linear system but cannot act on it, then 0-2 may be reduced to 0-0.
Today much of computer-human interaction is characterized by a learning system interacting with a simple linear process. You (the learning system) signal your computer (the simple linear process); it responds; you react. After signaling the computer enough times, you develop a model of how it works. You learn the system. But it does not learn you. We are likely to look back on this form of interaction as quite limited.
Search services work much the same way. Google retrieves the answer to a search query, but it treats your thousandth query just as it treated your first. It may record your actions, but it has not learned—it has no goals to modify. (This is true even with the addition of behavioral data to modify ranking of results, because there is only statistical inference and no direct feedback that asserts whether your goal has been achieved.)
**1-1 Balancing**
The output of one self-regulating system is input for another. If the output of the second system is measured by the first system (as the second measures the first), things are interesting. There are two cases, reinforcing systems and competing systems. Reinforcing systems share similar goals (with actuators that may or may not work similarly). An example might be two air conditioners in the same room. Redundancy is an important strategy in some cases. Competing systems have competing goals. Imagine an air conditioner and a heater in the same room. If the air conditioner is set to 75, and the heater is set to 65—no conflict. But if the air conditioner is set to 65 and the heater is set to 75, each will try to defeat the other. This type of interaction is balancing competing systems. While it may not be efficient, especially in an apartment, it’s quite important in maintaining the health of social systems, e.g., political systems or financial systems.
If 1-1 is open loop, that is, if the first system provides input to the second, but the second does not provide input to the first, then 1-1 may be reduced to 0-1.
**1-2 Managing and Entertaining**
The output of a self-regulating system becomes input for a learning system. If the output of the learning system also becomes input for the self-regulating system, two cases arise.
The first case is managing automatic systems, for example, a person setting the heading of an autopilot—or the speed of a steam engine.
The second variation is a computer running an application, which seeks to maintain a relationship with its user. Often the application’s goal is to keep users engaged, for example, increasing difficulty as player skill increases or introducing surprises as activity falls, provoking renewed activity. This type of interaction is entertaining—maintaining the engagement of a learning system.
If 1-2 or 2-1 is open loop, the interaction may be seen as essentially the same as the open-loop case of 0-2, which may be reduced to 0-0.
**2-2 Conversing**
The output of one learning system becomes input for another. While there are many possible cases, two stand out. The simple case is “it-referenced” interaction. The first system pokes or directs the second, while the second does not meaningfully affect the first.
More interesting is the case of what Pask calls “I/you-referenced” interaction: Not only does the second system take in the output of the first, but the first also takes in the output of the second. Each has the choice to respond to the other or not. Significantly, here the input relationships are not strict “controls.” This type of interaction is a like a peer-to-peer conversation in which each system signals the other, perhaps asking questions or making commands (in hope, but without certainty, of response), but there is room for choice on the respondent’s part. Furthermore, the systems learn from each other, not just by discovering which actions can maintain their goals under specific circumstances (as with a standalone second-order system) but by exchanging information of common interest. They may coordinate goals and actions. We might even say they are capable of design—of agreeing on goals and means of achieving them. This type of interaction is conversing (or conversation). It builds on understanding to reach agreement and take action [16].
There are still more cases. Two are especially interesting and perhaps not covered in the list above, though Boulding surely implies them:
+ learning systems organized into teams
+ networks of learning systems organized into communities or markets
The coordination of goals and actions across groups of people is politics. It may also have parallels in biological systems. As we learn more about both political and biological systems, we may be able to apply that knowledge to designing interaction with software and computers.
Having outlined the types of systems and the ways they may interact, we see how varied
interaction can be:
+ reacting to another system
+ regulating a simple process
+ learning how actions affect the environment
+ balancing competing systems
+ managing automatic systems
+ entertaining (maintaining the engagement of a learning system)
+ conversing
We may also see that common notions of interaction, those we use every day in describing user experience and design activities, may be inadequate. Pressing a button or turning a lever are often described as basic interactions. Yet reacting to input is not the same as learning, conversing, collaborating, or designing. Even feedback loops, the basis for most models of interaction, may result in rigid and limited forms of interaction.
By looking beyond common notions of interactions for a more rigorous definition, we increase the possibilities open to design. And by replacing simple feedback with conversation as our primary model of interaction, we may open the world to new, richer forms of computing.






11 Comments
jeremy yuille
Jan 31, 2009
6:22 pm
fantastic work! sorry I can’t comment deeper, on iPhone.
one thing I’m really digging here is the way you’ve integrated cybernetics into the interaction model. it’s been left out for too long, and is an important antecedent; though not all consuming, as some would argue.
this will be a great reading for students. thanks again.
Ivan Walsh
May 24, 2009
4:45 pm
Thank you for this excellent article.
Rolfe A. Leary
Jun 10, 2009
8:35 pm
Very interesting view of ‘interaction’. I’ve focused on biological interactions, and followed the works of Edward F. Haskell, who generalized the arrow diagrams in Einstein and Infeld (EofP), page 17, to produce an interaction based mathematical coordinate system (see cover of Main Currents in Modern Thought 7(2), 1949). Most biologists/ ecologists (like E.P.Odum) have used Haskell’s coaction cross tabulation of (+,-,0) that gives 9 types (groups). Others of us have used the mathematical coordinate system that includes both type, as well as intensity, of interaction (RALeary, Interaction theory in forest ecology and management, 1985; Mattson and Addy, Science, 1975; and others). I’m not certain if there is any overlap with the explanation of ‘interaction’ in this excellent piece. Just found it. Need more time to digest. Very nice website. Glad I found it.
See-ming Lee
Aug 11, 2009
2:52 pm
Great article, Hugh.
I find it particularly insightful that most of what we seen today is mostly reactive and lacking true interactive component.
Your analysis of of the different types of systems is very interesting. Thanks!
Ernest Edmonds
Jan 27, 2010
8:47 pm
Enjoyed it too. My paper below will probably be of interest in exactly the same area, as it covers the same issues.
Ernest
Edmonds, E. A. (2007). Reflections on the Nature of Interaction. CoDesign: International Journal of Co-Creation in Design and the Arts. Taylor & Francis Group, UK: September 2007, Vol. 3 Issue 3. pp 139-143.See http://www.informaworld.com/smpp/content~db=all~content=a772640193
madaksi siraji youngdool
Mar 2, 2010
1:23 am
it is nice
marie
Sep 27, 2010
10:17 am
not alot of help thanks!
Ussene Omar
Mar 17, 2011
2:11 am
I ejoyed it very much, and would to say that classroom interaction is crucial in particular for learning. what i have seen these days is that some language techers care about the classroom interation if so they lack awareness of it……!
Max Song
Jul 17, 2011
6:21 pm
This is a great piece, thank you for sharing. I’ve recently entered the world of computer programming, and could really appreciate your metaphors of
coding as a learning system interacting with a linear system.
Synthetic biology, on the other hand, and bioengineering are examples of a learning system interacting with a closed feedback loop system (a cell).
It is profoundly interesting what learning systems find “entertaining” though. From this perspective, ideas of pushing gamification are pretty low on the order chain. It seems more of a deception, that a simple feedback loop can control the attention of the learning system involved in it.
The highest order that you listed, conversing, is mostly limited to humans nowadays. And somewhere in there is the idea of subterfuge, or of not being able to completely understand something. As argument, imagine if that a computer program repeated broke the expectations of a user- the user would suspect that the program was “intelligent”. Or the challenges of interacting with other people, and the immense world of politics, of continuous anticipation and frustration.
Thanks again for the article, it has given me something great to think about 🙂
Hadi SABAAYON
Oct 4, 2012
2:28 am
Thank u for this interesting article. It clears the different models of interaction and i think that it helps in developping other concepts concerned by human-computer interaction and relationship.
mamaligadoc
Jan 2, 2021
10:30 am
With respect !!!